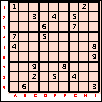
L’efficacité de l’analyse globale est dûe au fait :
- qu’on évalue une seule fois une petite liste de candidats qui concerne plusieurs cases d’une même zone,
- que l’étude d’une case à compléter consiste simplement à réduire cette liste déjà courte en analysant les autres zones contenant cette case,
- qu’implicitement, on considère donc l’interaction de tous les candidats de la liste (ce n’est plus une analyse candidat par candidat),
Commencez par les lignes, colonnes ou régions où il manque le moins de candidats à moins que vous n’ayez remarqué une particularité géométrique intéressante :
- il manque un candidat dans un ligne : placez le immédiatement.
- il en manque deux ? C’est une doublette à inscrire dans les deux trous ... et il n’est pas rare qu’en fait on arrive à placer ces deux candidats directement quand l’un deux est interdit dans un des deux trous,
- il en manque 3 ? c’est une triplette qui mérite d’être notée. Très souvent, l’un des chiffres se placera automatiquement à cause d’un bouchage de trou (voir la technique des murs troués).
- il en manque 4 ? Ne désespérez pas : vous pouvez avoir une bonne surprise.
- il en manque 5 ? Aïe aïe aïe : soit vous avez manqué quelque chose, soit vous avez affaire à un diabolique pervers (typique d’un 6 ou 7 étoiles). Dans ce dernier cas, il faut parfois en passer par là (voir les exemples de résolution de problèmes diaboliques).
Le plus difficile, au début, c’est de bien lister dans sa tête les candidats manquants. Mais ensuite c’est très efficace car vous n’avez plus à considérer que cette liste pour chaque trou de la zone étudiée. Ensuite il faut évidemment tenir compte du contexte pour savoir si tous les candidats apparaissent dans tous les trous (c’est heureusement rarement le cas).
Durant cette étape, il faudra être vigilant :
- ne pas mettre inutilement un candidat dans une case alors qu’il est déjà présent (parfois virtuellement seulement via une marque de choix directionnelle) dans la ligne perpendiculaire,
- essayer de repérer des doublettes et triplettes qui pourraient apparaître soudainement dans la zone étudiée ou dans les autres zones contenant les trous,
- exploiter ces doublettes et triplettes en supprimant les candidats inutiles,
- répercuter les suppressions de candidats sur les marques de choix. C’est souvent cette technique là, appelée "report de marque", qui débloque les SUDOKU complexes,
- ne pas oublier de remarquer la formation de murs encore que ce soit généralement moins important que pendant l’étape 1,
- penser au Swing qui peut survenir à tout moment.
Reprenons l’exemple employé pour décrire l’étape 1. A l’issue de cette première étape, voici la position normalement obtenue :
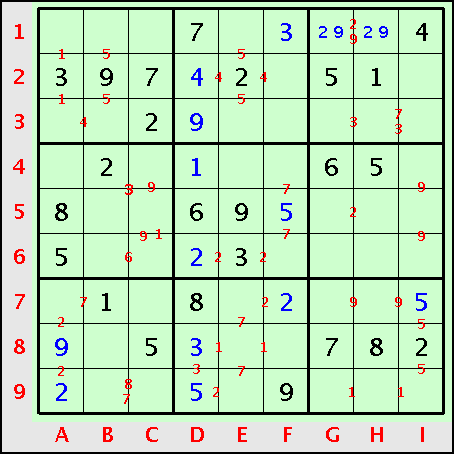
Cette position est convenable pour démarrer l’étape 3 en omettant l’étape 2 car le diagramme montre pas mal de lignes, de colonnes et de régions où il manque deux, trois ou quatre valeurs. Dans le cas où le diagramme ne montrerait que très peu (voire pas du tout) de lignes, colonnes ou régions suffisamment remplies, alors la stratégie correcte serait d’essayer les techniques de l’étape 2 qui sont justement prévues pour trouver des placements astucieux supplémentaires.
En attendant, commençons par la ligne L2 où il manque (68) pour poursuivre par R5 (478), L8 (146) et la colonne A (1467) :
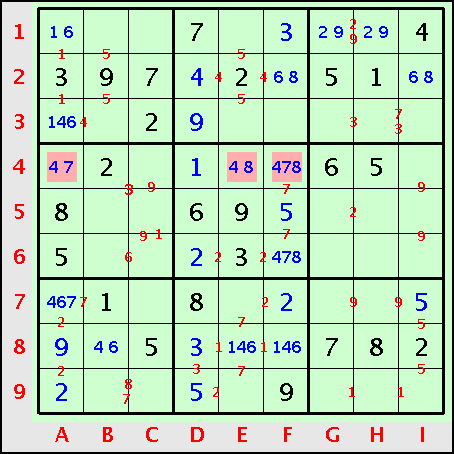
Ici on est un peu chanceux car on détecte une triplette 478 sur la ligne L4 dès le remplissage de la première zone à quatre tous. Naturellement, on aurait pu choisir de remplir une autre zone à quatre trous (lors de la résolution de ce problème, j’avais commencé par la région R7 qui ne montre rien de spécial). Mais tôt ou tard, la triplette serait apparu lors du remplissage de la colonne A.
Il s’agit maintenant de compléter immédiatement la ligne L4 et d’en tirer toutes les conséquences possibles :
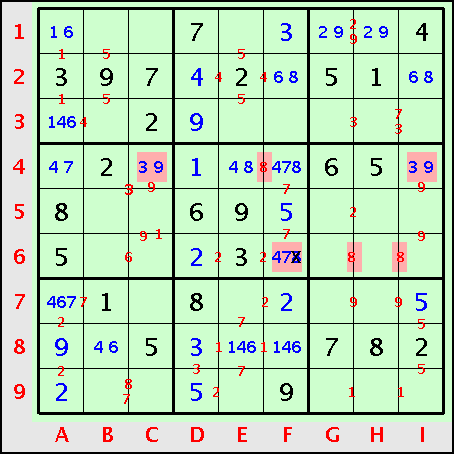
Évidemment, la ligne est complétée par le doublon 39. Mais ce n’est pas la conséquence principale. Il est absolument fondamental de mettre en évidence que le 8 de la ligne L4 se situe dans la région R5. C’est ce que j’appelle un report de marque des listes de candidats vers les marques de choix . Une fois établie la place approximative du 8 dans la région R5, il devient évident que le candidat 8 de la case F6 n’a plus sa place et peut être rayé. Par ailleurs, ce report de marque localise aussi le 8 dans la région R6.
On voit que chaque succès obtenu avec la technique principale de l’étape 2 doit être complété par un report de marque suivi d’une propagation des nouvelles marques de choix (technique typique de l’étape 1).
Et maintenant comment poursuivre ? On pourrait bien sûr continuer l’approche globale. Mais la réalisation rapide d’un SUDOKU demande de l’astuce. En particulier, la victoire obtenue par le report de marque précédent semble vraiment bien mince (suppression du candidat 8 de la case F6) ... à moins qu’il n’existe, dans la ligne 6 ou la colonne F, une surprise agréable.
Et un bon joueur se doit de jeter un oeil sur les cases correspondantes (c’est typiquement une technique normalement réservée à l’étape 2). La première case à analyser est sans doute la case F3 mais la liste des candidats associés (168) ne donne rien. Il faut chercher une case avec peu de candidats. Or une seule case de la ligne 6 est intéressante : celle sur la colonne H. En effet, les autres cases contiennent soit un 6, soit un 8 (ce sont les marques de choix qui l’indiquent) qui ne font pas bon ménage avec le doublon 47 ... Et, miracle, la case H6 ne peut contenir que 4 ou 7.
Naturellement, la ligne L6 doit d’être complétée d’urgence :
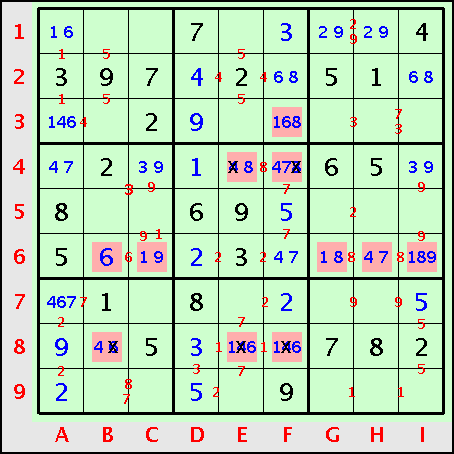
Le doublon 47 de la ligne L6 permet le placement direct du 6 en B6 avec un effet en cascade. Même l’essai de la case F3 se trouve récompensé par l’apparition du triplé 168 en colonne F, ce qui donne E4=8. La suite est un jeu d’enfant : il suffit de continuer l’approche globale méthodiquement.
Au passage, vous venez d’assister aux moments clés de la résolution d’un SUDOKU classé diabolique (5 étoiles au crash test).