par fj

Il m’a fallu trois jours et près de 5000 coups élémentaires pour enfin trouver la solution de ce SUDOKU démoniaque !
Cela le classe au niveau hallucinant de 100 étoiles (environ 50 coups par étoile). En écrivant cet article, j’ai toutefois rabaisser le nombre de coups à 2000, ramenant la difficulté au niveau plus modeste de 40 étoiles ... ce qui reste évidemment monstrueux, les SUDOKU des revues ne dépassant jamais 7 étoiles (350 coups au maximum) !
Prise en main du monstre
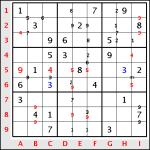
Voici la grille de départ :

La première étape de la stratégie de résolution amène le diagramme suivant :

Inutile de dire que les progrès ne sont pas brillants :
- un seul placement évident,
- une moisson minime de marques de choix.
Il est impossible en pratique de démarrer l’étape 3 (l’analyse globale) après un remplissage aussi pauvre d’une grille. La stratégie générale est ici la recherche de placements directs astucieux ou, à défaut, des listes courtes de candidats :

Voilà un résultat particulièrement frustrant :
- aucun placement direct supplémentaire,
- aucun doublé ou triplé,
- deux listes à deux candidats seulement : C5=34 et C2=46
Juste pour voir, la grille "complétée" devient :

Et comme de bien entendu, il n’y a rien de plus à l’horizon :
- pas de doublé,
- pas de triplé,
- pas de motif particulier exploitable,
- pas de groupe caché.
Doubles paris précoces
A situation exceptionnelle, méthodes exceptionnelles ! C’est pourquoi je tente de voir ce que donnent des doubles paris contraires, dès maintenant, avant tout remplissage. Le but n’est pas de résoudre la grille mais simplement de continuer à acquérir quelques connaissances sur son comportement démoniaque.
Double pari du 3 en R4 :

Il ne donne rien sinon le fait de rappeler que le 3 en R6 n’a que trois cases possibles, ce qu’on savait déjà !
Double pari du 7 en R5 :

Il ne donne strictement rien !
Double pari sur le 9 en R4 :

On note un double Swing perpendiculaire du 9 en R8, le pari rouge amenant le Swing en R88 tandis que le vert l’amène en R8E. Cela donne cette fois (enfin !) un premier indice précieux sur la grille : il n’y a pas de 9 dans les quatre cases de coin de la région 8, c’est à dire D7, F7, D9 et F9.
Double pari sur la case C5=34

Rien non plus, même si le 4 a bien débloqué la grille (il faudra s’en souvenir).
Stratégie
Après tout cela, le bilan est maigre : seul le pari du 9 en R4 a montré un petit résultat. En tout cas, il est clair que la grille en l’état est trop difficile pour moi et que rajouter un placement à 50% ne la rend pas plus facile. J’en déduis qu’il me faut au moins deux placements supplémentaires pour avoir une grille jouable (peut-être). Naturellement, deux placements à 50% chacun ne génèrent pas une grille mais quatre grilles dont trois d’entre elles n’ont pas de solution.
Je choisis donc le 9 en R4 (il m’a donné un petit résultat) et la case C5=34 : elle a montré une bonne propagation de marques.
Voici les quatre grilles simplifiées à résoudre :




Grille numéro 1
Première étape : l’analyse région par région
Passons à l’approche globale pour les zones à 3, 4 et 5 trous en commençant par l’alignement v1 où ont été ajoutés les placements.
- un triplé 278 apparaît rapidement en CB
- l’analyse de la colonne C donne C2=6. En association avec le triplé 278 précédent, on obtient B1=5
- doublé 59 en R22
- doublé 69 en R7B
- doublé 47 en L2 (A2 et G2) qui amène G2=1
Inutile d’essayer de remplir les régions R8 et R9 car les listes y sont trop longues :

A présent, il s’agit de réduire les listes. Or la meilleure technique pour cela est le double pari équilibré. La case D1=48 attire mon regard car les deux paris progressent tout de suite, surtout le vert (D1=4). Mais en regardant attentivement le pari rouge (D1=8), on note beaucoup de motifs intéressants :
- triplé 134 en L3 => A2=4
- motif de non unicité en A3=78 B3=78 A4=78 B4=278 => B4=2
- doublé 78 en B6/G6 => H6=5
- triplé 346 en colonne I
Le pari vert n’est pas en reste :
- toute le ligne 1 se résout,
- un doublé 47 apparaît en R3H
- il s’en suit un second motif de "presque" non unicité entre A2=47 A3=247 H2=47 et H3=47 => A3=2

Que tire-t-on de tout cela ? Beaucoup d’éléments si on applique méthodiquement les quatre théorèmes du double pari :
- d’abord les deux paris sont d’accord pour A2=4 et H2=7 : Ces deux placements sont donc corrects.
- ensuite le même chiffre est parfois choisi à des emplacements différents d’une même zone, comme le 2 en région 1 par exemple : seules ces deux cases sont alors possibles pour ce chiffre dans cette région et donc le 2 disparaît de la case B3.
- le troisième théorème s’applique dans les cases où les deux paris donnent des résultats différents. C’est le cas de la case H3 par exemple. Dans ce cas, les candidats non sélectionnés sont supprimés (candidat 7 de la case H3).
- le 4ème théorème est le plus subtil. Si des candidats différents dans des cases différentes d’une même zone sont sélectionnés par les deux paris, alors des éliminations sont possibles, le candidat du premier pari disparaissant de la case du second et réciproquement. C’est le cas par exemple des cases A4 et B4, le 2 de la case A4 et le 7 de la case B4 pouvant être éliminés. On retrouve encore ce motif entre les cases D5 et D6/E6 : le 7 disparaît de ces deux dernières cases. Mais cela marche aussi entre E3 (pari vert 1) et E6 (pari rouge 9) donc E6=9. D’une manière analogue, on remarque que le 8 vert de H4 (il est bel et bien vert même si j’ai oublié de le colorier sur le diagramme ci-dessus) détruit le 8 du pari rouge H6=5 ce qui valide d’ailleurs ce pari.

La grille s’est bien simplifiée mais il y a encore du travail, sans parler des deux régions R8 et R9 toujours vierges de placement. Ceci dit, on peut déjà insérer le doublon 59 en R9I.
Récidivons avec un nouveau double pari, par exemple dans la case F5 :

C’est beaucoup moins efficace. On ne remarque qu’un théorème 4 entre les cases E1 et E3 (pas de 3 en E4). Remplissons les cases restantes faute de mieux :

Que faire ? Je propose un troisième pari en région 8, E8=3 ou E9=3 par exemple.
- pour le premier pari, un doublon 59 D2/D8 surgit qui donne D5=7 puis D7=4 et D9=1. De plus un triplé 569 est mis en évidence en L9 (B9, E9, I9). En fait, toute la grille semble se résoudre avec E8=3 ... mais je m’arrête avant la fin.
- le second pari, au contraire, s’arrête très vite (résolution des 3 seulement).
Conclusion : menons le premier pari à son terme ... Et enfin une anomalie survient : deux 6 en colonne G. Donc F8=3 !

Heureusement, D8=9 avait été oublié pour le second pari et la grille progresse à nouveau. Elle se débloque presque complètement quand un doublon 16 surgit en R44 :

Et ici, il faut encore être bien éveillé pour noter le quadruplé 2468 en L7 (donc B7=9).

Voici le diagramme final : la case D7 est vide et la grille 1 n’a pas de solution.
La résolution de cette simple grille a demandé 986 coups élémentaires. Cela en fait la plus complexe que je n’ai jamais résolue (la précédente était un "9 étoiles" avec 450 coups !). Cela la classe au niveau 20. Quand on pense que c’est une grille nettement simplifiée par rapport à "Al Escargot" !
Grille numéro 2
L’analyse région par région est moins efficace qu’avec la grille précédente :

Mais l’analyse globale renverse un peu la situation. A noter :
- un triplé 278 en R4 qui permet le placement A4=4,
- un triplé 278 en colonne B,
- un report de marque du 7 en R4B qui empêche B3=7 et place un 7 en R1A.
Par analogie avec la grille précédente, les régions R8 et R9 sont laissées vierges :

Le premier pari de la grille 1 n’est plus possible (case D1). Mais la case B1 fait aussi bien l’affaire :
Le pari vert (B1=5) progresse grâce aux éléments suivants :
- un doublé 27 en R13
- un doublé 46 en L2 (C2/H2) qui permet le placement G2=1,
- un doublé 59 en R22,
- un triplé 134 en R2 qui donne D1=8
- un dernier doublé 46 en R1C qui n’apporte rien de particulier.
Le pari rouge (B1=6) montre :
- un doublé 28 en CC (C1/C6) ce qui donne C7=6,
- un doublé 28 en R7A qui amène A3=7,
- un doublé 19 en R22 et un doublé 67 en R32,
- le placement I3=1 et donc I4=6, F5=6, G6=1.

Et que tire-t-on de ce double pari bien équilibré ? Pratiquement rien du tout. Incroyable ! Je crois bien que c’est la première fois qu’un double pari équilibré m’apporte aussi peu de résultat : le théorème 4 sauve l’honneur en interdisant G2=4 (interaction C2/G2 des placements différents rouge et vert).
Comment des grilles 1 et 2 presque identiques peuvent-elles se comporter si différemment ?
Evidemment, il faut quand même persévérer. Dilemme : que choisir comme nouveau double pari ? J’ai le choix entre une autre case contenant deux candidats ou bien une marque désignant deux cases.
Après avoir été échaudé avec une case à deux candidats qui semblait prometteuse, j’opte cette fois pour une marque de choix. Quand on choisit une telle marque comme base d’un double pari, autant prendre celle désignant deux cases très chargées car cela élimine à chaque fois tous les autres candidats de la case choisie. Les meilleures marques sont donc le 2 en R3 et le 3 en R6. J’opte pour le 2 car il est plus près de l’action (car plus éloigné des régions désertées R8 et R9).
Et tout de suite le pari s’avère tout sauf équilibré. Le pari vert G1=2 est immédiatement stoppé alors que le pari rouge H3=2 semble débloquer totalement la grille ! En temps normal, j’aurais abandonné un pari aussi déséquilibré mais est-ce bien un SUDOKU normal ? Et il ne faut pas oublier que la fin de la résolution de la grille 1 s’est justement faite sur un pari déséquilibré.
Par ailleurs, ce pari donne tout de suite un résultat car le pari vert dit G1=2 tandis que le pari rouge conclut rapidement à G1=4. Le troisième candidat (6) de la case est donc éliminé (c’est déjà aussi bien que le pari précédent !). Donc faisons progresser le pari rouge en espérant une anomalie rapide :
- doublon 19 en R22
- doublon 67 en R32
Et sans la moindre difficulté, on obtient pratiquement la résolution complète des cases dotées d’une liste de candidats (dans les cases sans placement rouge, les candidats impossibles pour le pari rouge sont rayés pour faciliter la compréhension) :

Pas d’anomalie en vue. Mais compte tenu de l’ampleur de cette résolution, je ne doute plus que le pari rouge puisse aller au bout et afficher, vers la fin, l’anomalie attendue. Il est temps de compléter les régions R8 et R9 uniquement avec les candidats compatibles au pari rouge : inutile de s’embarrasser de listes complètes puisqu’on sait qu’au début du pari ces deux régions étaient vides ; on pourra donc restaurer facilement la position de départ.
Commençons par la région R9 plus simple à remplir que R8 :

Au tour de la région 8 en tenant compte du doublon 28 en L8 :

On voit le placement direct du 3 suivi de celui du 6. De plus il faut exploiter le doublon 59 en R88 et remarquer qu’il y a un triplé caché 124 dans la région R8 (ce qui amène la suppression des candidats rayés dans la région R8 du le diagramme ci-après) :
 .
.
Et c’est la plus grosse surprise du pari rouge : il est correct et la grille est résolue.
Décidément, c’est un problème à surprise. Le plus souvent, le volet d’un double pari qui progresse le plus est faux (la loi de Murphy appliquée au SUDOKU). Mais cette grille sort vraiment de l’ordinaire : c’est le pari qui progresse qui est le bon !
Au passage, j’ai plutôt de la chance puisque la solution est obtenue dès la seconde grille. Celle-ci a demandé un peu plus de 700 coups. En tenant compte des différents essais avant de définir la stratégie gagnante, il aura bien fallu les 2000 coups annoncés en début d’article !
Voici la grille résultat nettoyée :
 .
.